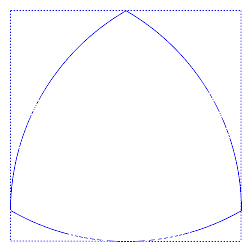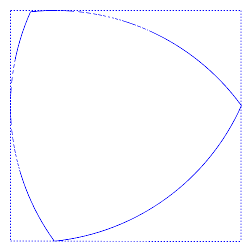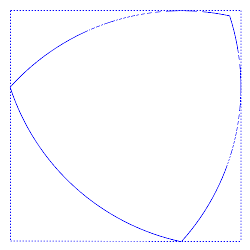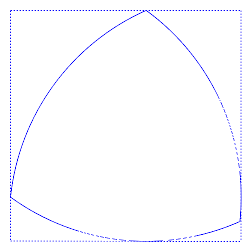
 Andriy Prymak et al. 2024/SageMath/Danylo Rádchenko. Una forma 3D de ancho constante vista desde tres ángulos diferentes. La vista central se asemeja a un triángulo de Reuleaux 2D.
Andriy Prymak et al. 2024/SageMath/Danylo Rádchenko. Una forma 3D de ancho constante vista desde tres ángulos diferentes. La vista central se asemeja a un triángulo de Reuleaux 2D. LA ETIQUETA DE TERRORISMO: UNA MANIOBRA DE TRUMP PARA INTERVENIR EN VENEZUELA, COLOMBIA Y MÉXICO26 Nov 2025 0 Comentarios
LA ETIQUETA DE TERRORISMO: UNA MANIOBRA DE TRUMP PARA INTERVENIR EN VENEZUELA, COLOMBIA Y MÉXICO26 Nov 2025 0 ComentariosTrump está usando un vacío legal para reconstruir la arquitectura de seguridad en el continenteNo se...
 LAS SIESTAS CORTAS, FACTOR FUNDAMENTAL PARA PRESERVAR LA SALUD DEL CEREBRO26 Nov 2025 0 Comentarios
LAS SIESTAS CORTAS, FACTOR FUNDAMENTAL PARA PRESERVAR LA SALUD DEL CEREBRO26 Nov 2025 0 ComentariosEste hábito podría contribuir con tu salud cerebral y reducir el riesgo de demenciaGettyimages.ruact...
 "UNA NUEVA IZQUIERDA REVOLUCIONARIA DEBE ANIMARSE A SOLTAR LASTRES"26 Nov 2025 0 Comentarios
"UNA NUEVA IZQUIERDA REVOLUCIONARIA DEBE ANIMARSE A SOLTAR LASTRES"26 Nov 2025 0 ComentariosEntrevista con Néstor KohanLas izquierdas latinoamericanas maquillaban la ideología burguesa, depend...
 AGUA POTABLE DEL AIRE Y EN TIEMPO RÉCORD26 Nov 2025 0 Comentarios
AGUA POTABLE DEL AIRE Y EN TIEMPO RÉCORD26 Nov 2025 0 ComentariosCómo funciona el innovador dispositivo desarrollado por el MITUna nueva tecnología ultrasónica convi...
 EL EJE EPSTEIN ES PEDOFILIA, ESPIONAJE, CHANTAJE Y BANCA26 Nov 2025 0 Comentarios
EL EJE EPSTEIN ES PEDOFILIA, ESPIONAJE, CHANTAJE Y BANCA26 Nov 2025 0 Comentarios¡La cibermilitarización globalista de la pedofilia!Sexo/Dinero/PoderAlfredo Jalife Rahme , geopolíti...
 MUERTE A LAS 'CÉLULAS ZOMBI': DESCUBREN UN POSIBLE TRATAMIENTO PARA LA DIABETES TEMPRANA26 Nov 2025 0 Comentarios
MUERTE A LAS 'CÉLULAS ZOMBI': DESCUBREN UN POSIBLE TRATAMIENTO PARA LA DIABETES TEMPRANA26 Nov 2025 0 ComentariosSu aplicación abre la puerta para abordar distintos aspectos del envejecimiento y las enfermedades a...
 LOS DATOS CLAVES QUE SITÚAN A VENEZUELA EN EL TOP DE LOS RECURSOS ESTRATÉGICOS26 Nov 2025 0 Comentarios
LOS DATOS CLAVES QUE SITÚAN A VENEZUELA EN EL TOP DE LOS RECURSOS ESTRATÉGICOS26 Nov 2025 0 ComentariosLas autoridades de la nación suramericana han advertido que las agresiones de EE.UU. en el Caribe ti...
 DESCUBREN UN ORGANISMO COMPLETAMENTE NUEVO DE LA VIDA26 Nov 2025 0 Comentarios
DESCUBREN UN ORGANISMO COMPLETAMENTE NUEVO DE LA VIDA26 Nov 2025 0 ComentariosSe ha descubierto un organismo que podría representar una rama completamente nueva en el árbol de la...
 LA EMANCIPACIÓN DE LA MUJER NO SE LOGRARÁ SIN TRANSFORMACIÓN RADICAL DEL SISTEMA QUE GENERA POBREZA, DESIGUALDAD, SUPEREXPLOTACIÓN Y MERCANTILIZACIÓN 25 Nov 2025 0 Comentarios
LA EMANCIPACIÓN DE LA MUJER NO SE LOGRARÁ SIN TRANSFORMACIÓN RADICAL DEL SISTEMA QUE GENERA POBREZA, DESIGUALDAD, SUPEREXPLOTACIÓN Y MERCANTILIZACIÓN 25 Nov 2025 0 Comentarios25N Construir la Organización Revolucionaria de las MujeresLa raíz de la opresión está en el capital...
 ¿TRES CONSCIENCIAS EN UNA? UN MODELO EVOLUTIVO REPLANTEA EL MISTERIO DE LA MENTE25 Nov 2025 0 Comentarios
¿TRES CONSCIENCIAS EN UNA? UN MODELO EVOLUTIVO REPLANTEA EL MISTERIO DE LA MENTE25 Nov 2025 0 ComentariosLa consciencia no sería un evento mágico restringido a nuestro córtex, sino una compleja alarma evol...
 ESTADOS UNIDOS: DE PRESIONES DIPLOMÁTICAS Y ECONÓMICAS A PREPARATIVOS PARA UNA AGRESIÓN MILITAR DIRECTA A VENEZUELA25 Nov 2025 0 Comentarios
ESTADOS UNIDOS: DE PRESIONES DIPLOMÁTICAS Y ECONÓMICAS A PREPARATIVOS PARA UNA AGRESIÓN MILITAR DIRECTA A VENEZUELA25 Nov 2025 0 ComentariosDOSSIER: La excusa la lucha contra el narcotráficoTrump prepara el terreno para intervenir en V...
 UNA NUEVA TECNOLOGÍA DESVELA LA MITAD OCULTA DEL GENOMA HUMANO25 Nov 2025 0 Comentarios
UNA NUEVA TECNOLOGÍA DESVELA LA MITAD OCULTA DEL GENOMA HUMANO25 Nov 2025 0 ComentariosEl mal llamado "ADN basura" podría permitir el desarrollo de nuevas terapias oncológicas y mejorar l...
 LA MATRIOSKA EUROPEA DE LA IRRELEVANCIA25 Nov 2025 0 Comentarios
LA MATRIOSKA EUROPEA DE LA IRRELEVANCIA25 Nov 2025 0 ComentariosLa combinación UE/OTAN no puede sino desempeñar el papel de chihuahuas patéticos y ladradores. Ese e...
 EL CACAO Y EL TÉ PUEDEN PROTEGER TU CORAZÓN DE LOS DAÑOS OCULTOS DEL SEDENTARISMO25 Nov 2025 0 Comentarios
EL CACAO Y EL TÉ PUEDEN PROTEGER TU CORAZÓN DE LOS DAÑOS OCULTOS DEL SEDENTARISMO25 Nov 2025 0 ComentariosLos flavonoles pueden ofrecer un atajo dietético sencillo para proteger las arterias de los peligros...
Trump está usando un vacío legal para reconstruir la arquitectura de seguridad en el continenteNo se...

 Andriy Prymak et al. 2024/SageMath/Danylo Rádchenko. Una forma 3D de ancho constante vista desde tres ángulos diferentes. La vista central se asemeja a un triángulo de Reuleaux 2D.
Andriy Prymak et al. 2024/SageMath/Danylo Rádchenko. Una forma 3D de ancho constante vista desde tres ángulos diferentes. La vista central se asemeja a un triángulo de Reuleaux 2D.
Trump está usando un vacío legal para reconstruir la arquitectura de seguridad en el continente No …



















