¿EXPLICAR EL PODER DE MANIPULAR EL ESPACIO-TIEMPO?

RUBÉN SIERRA 

20minutos.es/17 ene 2026 - 08:41

Imaginar situaciones de cómic y peleas intensas y alucinantes entre personajes siempre mola, jugando con un ‘¿Tú tienes este poder?¡Pues el mío es este y es mejor!’ pero… con coherencia. No puede ser un órdago y se acabó. Se tiene que respetar una escala de poder.

Si tú pegas un puñetazo, yo te doy una patada, que es más fuerte. Si tu lanzas un rayo, yo dos y de color morado, que es más intenso ¿tiene que ver en el poder el que sea de color morado? No, pero mola más y por eso hace más daño.

Poco a poco muestras que tus personajes tienen capacidades consecuentes y que crecen gradualmente. Menos si controlan el espacio-tiempo. Ahí estás regando fuera del tiesto y la escala de poder se ha ido a freír espárragos; algo que sucedió con la obra Jujutsu Kaisen y uno de sus personajes: Satoru Gojo, cuyo poder inicial estaba basado en una paradoja filosófica y luego la ciencia le dijo "lo siento, pero no". El estreno de la tercera temporada de esta serie es el mejor momento para explicar uno de los poderes más rotos del mundo de la ficción.

El autor de la obra, Gege Akutami, intentó (recalco el: intentó) darle una explicación lógica a sus habilidades basándose en física, matemáticas y filosofía, más o menos. Entre los capítulos de su obra incluye pequeñas explicaciones a partes de la historia, siendo una de ellas la de lógica de la técnica Infinito. Con ella, Gojo puede impedir que cualquier cosa lo toque, generando entre él y su oponente una barrera invisible que se divide infinitamente, ralentizando todo ataque a medida que se acerca. De primeras, es un ataque alucinante y muy, pero que muy poderoso, cuya base es la paradoja de Aquiles y la tortuga y que merece la pena disertar para ver cómo filosóficamente es una muy buena explicación, pero científicamente… No tanto. La paradoja cita lo siguiente: "Aquiles da ventaja a una tortuga en una carrera. Si el empieza en la zona inicial, el animal empieza un poco más adelantado. Cuando Aquiles recorre la distancia que separaba a ambos, la tortuga ha avanzado un poco más. Cuando Aquiles alcanza esa nueva posición, la tortuga sigue moviéndose. Y así, según Zenón, de forma infinita, porque el espacio entre ellos siempre puede dividirse en partes más pequeñas".

Lo interesante es que en la Grecia clásica no existía el concepto de límite o de convergencia infinita como lo entendemos hoy. Para Zenón, si una tarea se puede dividir en infinitas partes, debía necesitar un tiempo infinito para completarse.

Esto planteaba un conflicto directo con nuestra experiencia cotidiana, donde Aquiles efectivamente puede alcanzar a una tortuga sin problemas porque la tortuga es lenta y con dos zancadas ya estás por delante de ella. La paradoja entonces no buscaba defender que Aquiles fuese más lento, sino atacar la lógica del movimiento continuo y divisible.

Filosóficamente, la paradoja servía para apoyar las ideas de Parménides, quien defendía que el cambio y el movimiento eran ilusorios. Si, como parece razonable, el espacio es infinitamente divisible, entonces movernos de un punto a otro implicaría recorrer infinitos tramos, y como infinitos no se pueden sumar para obtener un valor finito (o al menos eso creían), el movimiento sería una ilusión perceptiva. Un buen argumento para la época, aunque, con la formalización del cálculo infinitesimal, se pudo ver que lo que se creía infinito es, en realidad, finito.

A la suposición anterior donde se había mencionado que Aquiles le daba cierta ventaja, le vamos a poner una cifra. Supongamos que la tortuga parte 10 metros por delante, que Aquiles corre a una velocidad constante de 10 metros por segundo y que la tortuga avanza a 1 metro por segundo. En el momento en que comienza la carrera, la tortuga ya está a 10 metros de Aquiles. Él recorre esa distancia inicial en exactamente 1 segundo, pero mientras Aquiles cubre esos 10 metros, la tortuga también se desplaza, aunque solo 1 metro, llegando a los 11 metros respecto del inicio. A Aquiles y la tortuga les separa únicamente 1 metro.

Aquiles, imparable, recorre ese metro extra en solo 0,1 segundos, pero en ese breve instante la tortuga avanza de nuevo, esta vez 0,1 metros, ubicándose en el metro 11,1. Ahora les separa 0,1 metros, es decir, 10 centímetros.

Aquiles anda otra vez y cubre esa nueva distancia de 0,1 metros en apenas 0,01 segundos, momento en el cual la tortuga se ha desplazado a 11,11 metros, apenas 0,01 metros más, siendo su separación de 1 mero centímetro. Este proceso se repite una y otra vez, dando como resultado que, cada vez que Aquiles alcanza el punto donde estaba la tortuga, ella ya ha avanzado una fracción diminuta, por mínima que sea.

Si seguimos sumando estos tiempos: 1 segundo, 0,1 segundos, 0,01 segundos, 0,001 segundos, y así sucesivamente, observamos que la suma de todos ellos no se extiende hacia el infinito, sino que se aproxima cada vez más a un valor finito. En este caso, la suma total converge a aproximadamente 1,111 segundos, un número finito, aunque implique infinitos pasos intermedios. Lo mismo ocurre si se suman las distancias. Aunque el espacio entre Aquiles y la tortuga se pueda dividir teóricamente en infinitas partes, la suma de esas fracciones termina teniendo un valor limitado y alcanzable.

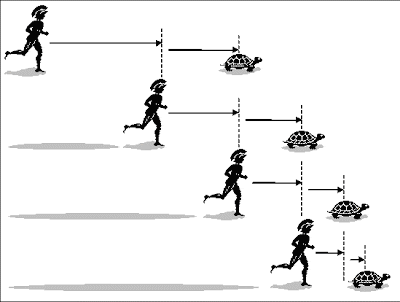
Representación de la paradoja de Aquiles y la TortugaCiencia como nunca

En este post de mi perfil de Patreon tenéis acceso a todas las cuentas para obtener este resultado, de libre acceso y gratuito. La paradoja se resuelve al comprender que una sucesión infinita de tiempos cada vez más pequeños, o de distancias decrecientes, puede tener una suma total que no es infinita. Aunque se añadan infinitos términos, si cada término es progresivamente menor, el total converge hacia un valor concreto. De este modo, Aquiles no solo alcanza a la tortuga en un tiempo razonable, sino que la supera poco después, desmontando la paradoja desde un punto de vista matemático.

Todo este lío se podía haber enfocado de otra manera si Gege Akutami hubiera mencionado que el poder de su personaje más poderoso no era similar al de la paradoja de Aquiles y la Tortuga, si no a otro elemento matemático.

¿Cómo se podía haber mencionado una analogía mejor para el poder Infinito de Satoru Gojo? Diciendo que es asintótico.

La técnica Infinito de Satoru Gojo funciona creando divisiones infinitas en el espacio entre él y su oponente, pero con una diferencia crucial: en lugar de permitir que la suma de esas divisiones tienda a un valor finito (como en el caso de Aquiles), mantiene la sucesión abierta indefinidamente, impidiendo que se complete. Te acercas, pero nunca llegas. Te acercas muchísimo, pero nunca del todo. Está a un palmo de ti, pero muy lejos a la vez.

En matemáticas, una asíntota es una recta a la que una función matemática se aproxima cada vez más, pero que nunca toca. Esto ocurre, por ejemplo, en la gráfica de una función que se acerca a cero pero sin llegar a ser exactamente cero. Lo que hace Gojo es convertir el espacio entre su cuerpo y cualquier amenaza en un límite asintótico: a medida que algo se acerca, el espacio-tiempo se divide infinitamente, ralentizando ese acercamiento hasta hacerlo prácticamente nulo, sin llegar nunca al contacto.

Tipos de asintotawww.disfrutalasmatematicas.com

Es una aplicación práctica de una idea antigua: el infinito no como algo inalcanzable, sino como una herramienta para crear imposibilidad física. Si cada intento de alcanzar un objetivo se encuentra con una nueva fracción del espacio, y ese proceso de división nunca se detiene, el contacto jamás se produce. Matemáticamente, aunque la serie de distancias podría converger, la técnica de Gojo funciona como si siempre añadiéramos un nuevo término antes de completar la suma. Por eso, más que emular a Aquiles y la tortuga, Gojo se comporta como una asíntota viviente.

Jujutsu Kaisen no es una mala obra, ni muchísimo menos. Sus personajes son carismáticos, su trama es misteriosa y llamativa y sus peleas alucinantes y brutales. ¿Qué tiene de malo? Algunas habilidades y su escala de poder. Todo fluye perfectamente y se la recomiendo a todas las personas con ganas de ver algo que merezca la pena… Salvo ese pequeño factor que, irónicamente, es el talón de Aquiles de la trama.